- El teorema de Pitágoras establece la relación entre los lados de un triángulo rectángulo.
- Sus aplicaciones van desde la construcción hasta la navegación y el diseño de interiores.
- Permite calcular distancias, alturas y longitudes mediante la relación entre catetos e hipotenusa.
- Es crucial en diversas disciplinas como ingeniería, jardinería y deportes.
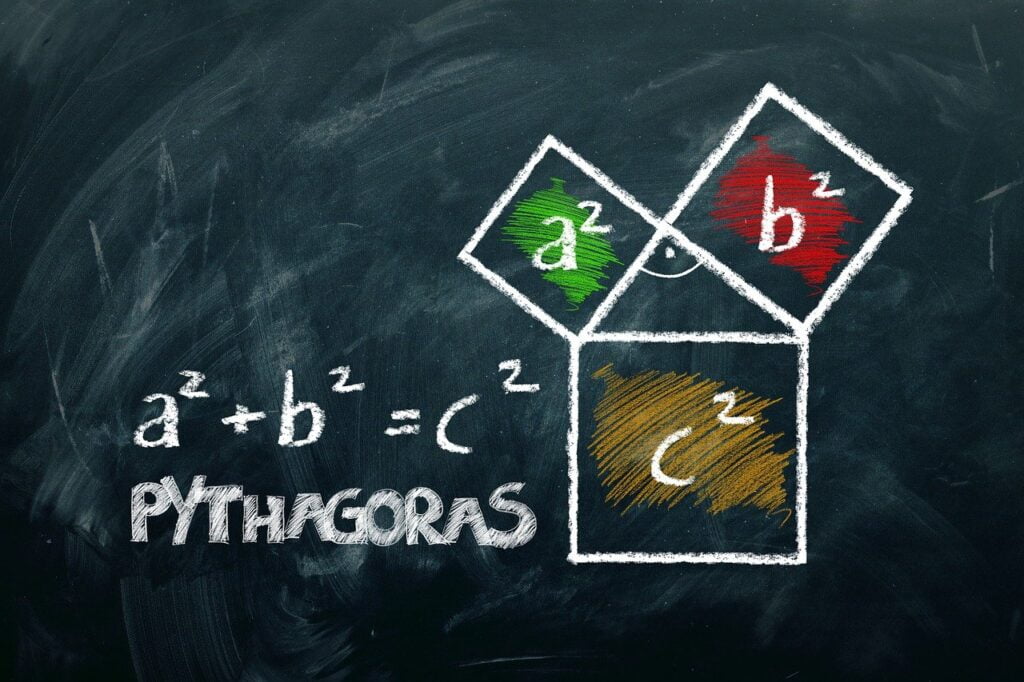
Introducción – Fórmula del Teorema de Pitágoras y ejemplo
Explicación
- Determinar distancias: En la vida real, como la longitud de una escalera necesaria para alcanzar una cierta altura.
- Problemas de navegación y geografía: Para encontrar la distancia más corta entre dos puntos.
- Aplicaciones en física: Calcular desplazamientos y trayectorias.
Ejemplo
El Teorema de Pitágoras en la Vida Cotidiana
1. El teorema de Pitágoras en la construcción
1.1. Cálculo de la longitud de las escaleras
1.2. Diseño de techos inclinados
1.3. Determinación de la altura de los edificios
2.1. Cálculo de distancias en el mar
2.2. Determinación de la altura de los faros
3. El teorema de Pitágoras en el diseño de interiores
3.1. Cálculo de la diagonal de una habitación
3.2. Diseño de muebles
3.3. Colocación de cuadros y decoraciones
4. Aplicaciones del teorema de Pitágoras en la jardinería
4.1. Diseño de parcelas y jardines
4.2. Cálculo de la longitud de las mangueras
4.3. Determinación de la altura de los árboles
5. El teorema de Pitágoras en el deporte
5.1. Cálculo de distancias en el golf
5.2. Determinación de la trayectoria de la pelota en el béisbol
5.3. Diseño de pistas de atletismo
Preguntas frecuentes sobre el Teorema de Pitágoras en la vida cotidiana
- ¿Qué es el teorema de Pitágoras? El teorema de Pitágoras es un principio matemático que establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados (catetos).
- ¿Cómo se formula el teorema de Pitágoras? La fórmula del teorema del teorema de Pitágoras se expresa como: a^2 + b^2 = c^2, donde «a» y «b» son las longitudes de los catetos, y «c» es la longitud de la hipotenusa.
- ¿Qué tipos de triángulos se pueden resolver con el teorema de Pitágoras? El teorema de Pitágoras se aplica específicamente a los triángulos rectángulos, es decir, triángulos que tienen un ángulo recto (90 grados).
- ¿Es posible utilizar el teorema de Pitágoras en formas que no sean triángulos rectángulos? No, el teorema de Pitágoras solo se aplica a triángulos rectángulos. Sin embargo, es posible descomponer otras formas geométricas en triángulos rectángulos para aplicar el teorema.
- ¿Cómo se puede aplicar el teorema de Pitágoras en la vida cotidiana? El teorema de Pitágoras tiene muchas aplicaciones en la vida cotidiana, como en la construcción (para calcular la longitud de escaleras o el diseño de techos inclinados), la navegación (para calcular distancias), el diseño de interiores (para calcular diagonales de habitaciones), la jardinería (para diseñar parcelas y jardines) y el deporte (para calcular distancias en el golf o la trayectoria de la pelota en el béisbol).
- ¿Qué otros campos, además de los mencionados en el artículo, utilizan el teorema de Pitágoras? Además de los campos mencionados en el artículo, el teorema de Pitágoras se utiliza en muchas otras áreas, como la astronomía (para calcular distancias entre cuerpos celestes), la ingeniería (para diseñar estructuras y maquinaria), la física (para analizar vectores y fuerzas), la cartografía (para crear mapas precisos) y la informática (para el diseño de gráficos y videojuegos).
Conclusión de Teorema de Pitágoras en la vida cotidiana
Tabla de Contenidos
- Introducción – Fórmula del Teorema de Pitágoras y ejemplo
- El Teorema de Pitágoras en la Vida Cotidiana
- Preguntas frecuentes sobre el Teorema de Pitágoras en la vida cotidiana
- Conclusión de Teorema de Pitágoras en la vida cotidiana